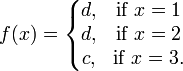แนวคิดที่สำคัญที่สุดคือ ฟังก์ชันนั้นเป็น "กฎ" ที่กำหนด ผลลัพธ์โดยขึ้นกับสิ่งที่นำเข้ามา ต่อไปนี้เป็นตัวอย่าง
"กฎ" ที่นิยามฟังก์ชันอาจเป็น สูตร, ความสัมพันธ์ (คณิตศาสตร์) หรือเป็นแค่ตารางที่ลำดับผลลัพธ์กับสิ่งที่นำเข้า ลักษณะเฉพาะที่สำคัญของฟังก์ชันคือมันจะมีผลลัพธ์เหมือนเดิมตลอดเมื่อให้สิ่งนำเข้าเหมือนเดิม ลักษณะนี้ทำให้เราเปรียบเทียบฟังก์ชันกับ "เครื่องกล" หรือ "กล่องดำ" ที่จะเปลี่ยนสิ่งนำเข้าไปเป็นผลลัพธ์ที่ตายตัว เรามักจะเรียกสิ่งนำเข้าว่า อาร์กิวเมนต์ (argument) และเรียกผลลัพธ์ว่า ค่า (value) ของฟังก์ชัน
เป็นฟังก์ชันที่นำตัวเลข x และ y มาหาผลคูณ ดูเหมือนว่านี่ไม่ใช่ฟังก์ชันจริงๆดังที่เราได้อธิบายข้างต้น เพราะว่า "กฎ" ขึ้นอยู่กับสิ่งนำเข้า 2 สิ่ง อย่างไรก็ตาม ถ้าเราคิดว่าสิ่งนำเข้า 2 สิ่งนี้เป็น คู่อันดับ  1 คู่ เราก็จะสามารถแปลได้ว่า g เป็นฟังก์ชัน โดยที่อาร์กิวเมนต์คือคู่อันดับ
1 คู่ เราก็จะสามารถแปลได้ว่า g เป็นฟังก์ชัน โดยที่อาร์กิวเมนต์คือคู่อันดับ  และค่าของฟังก์ชันคือ
และค่าของฟังก์ชันคือ 
 1 คู่ เราก็จะสามารถแปลได้ว่า g เป็นฟังก์ชัน โดยที่อาร์กิวเมนต์คือคู่อันดับ
1 คู่ เราก็จะสามารถแปลได้ว่า g เป็นฟังก์ชัน โดยที่อาร์กิวเมนต์คือคู่อันดับ  และค่าของฟังก์ชันคือ
และค่าของฟังก์ชันคือ 
ในทางคณิตศาสตร์ "ฟังก์ชัน" บัญญัติขึ้นโดย ไลบ์นิซ ใน พ.ศ. 2237 เพื่ออธิบายปริมาณที่เกี่ยวข้องกับเส้นโค้ง เช่น ความชันของเส้นโค้ง หรือจุดบนเส้นโค้ง ฟังก์ชันที่ไลบ์นิซพิจารณานั้นในปัจจุบันเรียกว่า ฟังก์ชันที่หาอนุพันธ์ได้
ฟังก์ชัน f จากข้อมูลนำเข้าในเซต X ไปยังผลที่เป็นไปได้ในเซต Y (เขียนเป็น  ) คือความสัมพันธ์ ระหว่าง X กับ Y ซึ่ง
) คือความสัมพันธ์ ระหว่าง X กับ Y ซึ่ง
 ) คือความสัมพันธ์ ระหว่าง X กับ Y ซึ่ง
) คือความสัมพันธ์ ระหว่าง X กับ Y ซึ่ง
- สำหรับทุกค่า x ใน X จะมี y ใน Y ซึ่ง x f y (x มีความสัมพันธ์ f กับ y) นั่นคือ สำหรับค่านำเข้าแต่ละค่า จะมีผลลัพธ์ใน Y อย่างน้อย 1 ผลลัพธ์เสมอ
- ถ้า x f y และ x f z แล้ว y = z นั่นคือ ค่านำเข้าหลายค่าสามารถมีผลลัพธ์ได้ค่าเดียว แต่ค่านำเข้าค่าเดียวไม่สามารถมีผลลัพธ์หลายผลลัพธ์ได้
 โดยที่แต่ละค่าของ xใน X จะมี y ใน Y ที่แตกต่างกัน โดยที่คู่อันดับ (x, y) อยู่ใน f
โดยที่แต่ละค่าของ xใน X จะมี y ใน Y ที่แตกต่างกัน โดยที่คู่อันดับ (x, y) อยู่ใน f
ดูตัวอย่างต่อไปนี้
 ความสัมพันธ์นี้เป็นฟังก์ชันจาก X ไปยัง Y เราสามารถหานิยามฟังก์ชันนี้อย่างชัดแจ้งได้เป็น f={ (1,d) , (2,d) , (3,c) } หรือเป็น
ความสัมพันธ์นี้เป็นฟังก์ชันจาก X ไปยัง Y เราสามารถหานิยามฟังก์ชันนี้อย่างชัดแจ้งได้เป็น f={ (1,d) , (2,d) , (3,c) } หรือเป็นโดเมน, โคโดเมน และเรนจ์[แก้]
X ซึ่งคือเซตข้อมูลนำเข้าเรียกว่า โดเมนของ f และ Y ซึ่งคือเซตของผลลัพธ์ที่เป็นไปได้ เรียกว่า โคโดเมน เรนจ์ของ f คือเซตของผลลัพธ์จริงๆ{f (x) : x ในโดเมน} ระวังว่าบางครั้งโคโดเมนจะถูกเรียกว่าเรนจ์ เนื่องจากความผิดพลาดจากการจำแนกระหว่างผลที่เป็นไปได้กับผลจริงๆ
ฟังก์ชันหนึ่งต่อหนึ่ง ฟังก์ชันทั่วถึง และฟังก์ชันหนึ่งต่อหนึ่งทั่วถึง[แก้]
- ฟังก์ชันหนึ่งต่อหนึ่ง (1-1) ฟังก์ชันจะคืนค่าที่ไม่เหมือนกันหากนำเข้าค่าคนละค่ากัน กล่าวคือ ถ้า x1 และ x2 เป็นสมาชิกของโดเมนของ f แล้ว f(x1) = f (x2) ก็ต่อเมื่อ x1 = x2
- ฟังก์ชันทั่วถึง (แบบ onto) ฟังก์ชันจะมีเรนจ์เท่ากับโคโดเมน กล่าวคือ ถ้า y เป็นสมาชิกใดๆของโคโดเมนของ f แล้วจะมี x อย่างน้อย 1 ตัว ซึ่ง f(x) = y
- ฟังก์ชันหนึ่งต่อหนึ่งทั่วถึง เป็นฟังก์ชันที่เป็นทั้งฟังก์ชันหนึ่งต่อหนึ่ง และฟังก์ชันทั่วถึง มักจะใช้แสดงว่าเซต X และเซต Y มีขนาดเท่ากัน